University of Technology Ilkka

Mat - 1.128 Elements of Discrete Mathematics

lst partial examination 19.3.1996

Write first clearly on each sheet of paper

- Elem. of discr. math., lst part. exam. 19.3.1996

- Student identification number, family name, given names

- Faculty

- Changes in name or faculty, if there are any

- Signature

1. Evaluate the sum

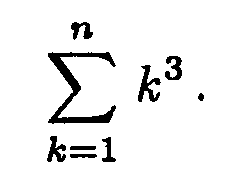
2. Red, yellow, and/or green balls are put in the vertices of a

regular pentagon, and fixed to its center by sticks which are colored with some of the same colours. How many different colorings is it possible to produce, if we can freely turn the pentagon in all three dimensions? How many colorings are there, if there are as many green as yellow parts? Use Polya's theorem to solve the problem.

3. All the degrees of the vertices in a connected linear planar graph G = (V, , E) are > 4, and the number of the regions in its planar embedding is r , the infinite region included. What is the minimal number of vertices in G ?

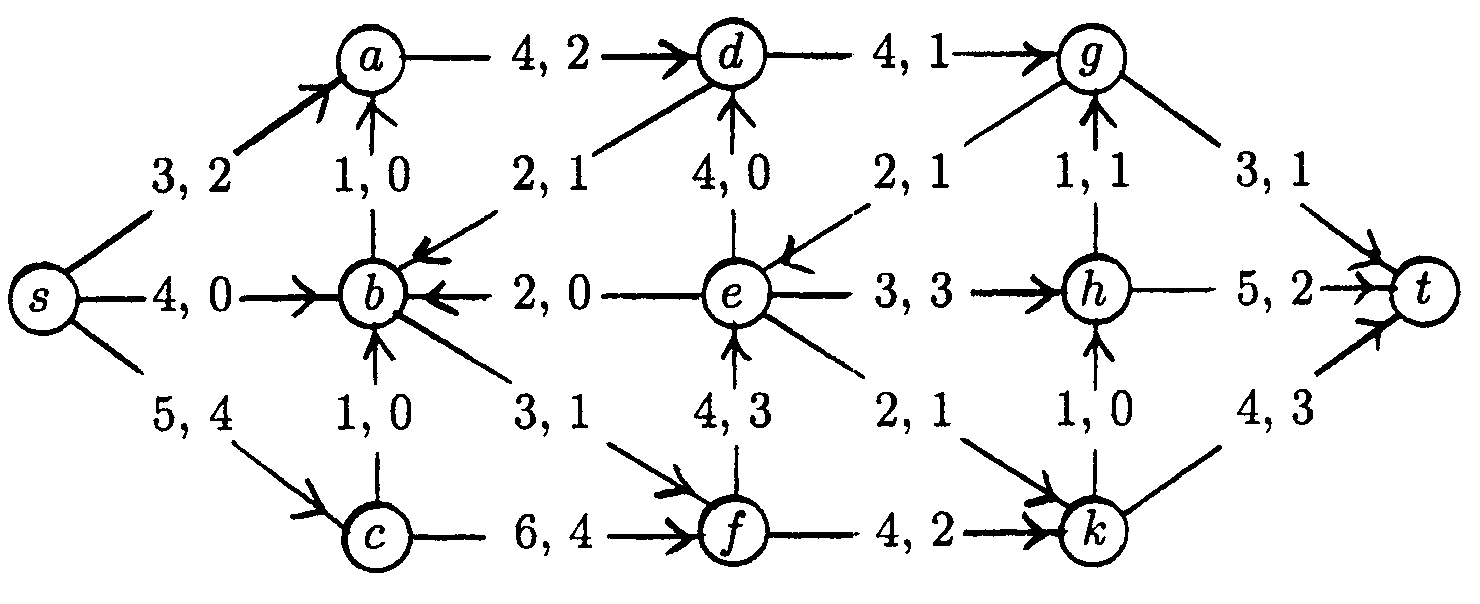
4. The following network is provided with the capasities of the edges and an initial flow. Maximize the flow with a suitable algorithm, and find a minimal cut.