Teknillinen korkeakoulu Ilkka
Mat - 1.128 Diskreetin matematiikan perusteet
Tentti 25.11.1996
Kirjoita ensin allamainitussa järjestyksessä koepapereihin selvästi
- Diskr. mat. per., tentti 25.11.1996
- Opiskelijatunnus, TEKSTATEN sukunimi, kaikki etunimet
- Koulutusohjelma (Ke, Ko, M, Mk, P, R, S, Tf, Ti, Tu)
- Mahdolliset entiset nimet ja koulutusohjelmat
- Nimikirjoitus
1. a) Laske arvo summalle
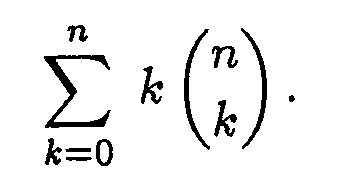
b) Osoita, että positiivisen kokonaisluvun r+k osituksia k :n positiivisen kokonaisluvun summaksi on yhtä monta kuin r :n osituksia yhteenlaskettaviksi, jotka ovat < k.
2. Helminauha,jossa on 16 helmeä,valmistetaan valkoisista ja mustista helmistä. Miten monta sellaista nauhaa voidaan tehdä, joissa on parittomat määrät kumpaakin väriä olevia helmiä? Nauhaa voi käännellä vapaasti kaikkiin asentoihin.
3. Olkoon G = (V, E) suunnistamaton lineaarinen graafi, jossa on n kärkeä. Oletetaan lisäksi, että G on itsekomplementaarinen, eli G ~ G.
a) Montako sivua G :ssä on?
b) Osoita, että n = 4k, tai n =4k+l, jollakin k E Z+.
4. Laske a) (p - 3)! (mod p), kun p <> 2 on alkuluku.
b) 31212 (mod 175).
5. Etsi jaottomat tekijät polynomille
P(x) = x5 + t x2 + (t + 1) x + (t + 1)
polynomirenkaassa, jonka kerroinkunta on
GF(4) = {0, 1, t, t + 1 | (mod 2), (mod (t2 + t + 1))}.