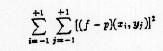
Kirjoita ensin allamainitussa järjestyksessä koepapereihin selvästi

- Num.anal.A, tentti 13.01.1994

- op.kirjan no., TEKSTATEN sukunimi ja etunimet puhuttelunimi alleviivattuna

- koulutusohjelma ja vuosikurssi (I,II,III,IV,N)

- mahdolliset entiset nimet ja koulutusohjelmat

- nimikirjoitus

1. Kun e on itseisarvoitaan hyvin pieni, on polynomin

p(x)=(x-1)(x-2)...(x-6)+ex^6

eräs juuri likimain 1 + ae. Laske a.

2. Määrää funktion f(x) = e^x kolmannen asteen Hermiten interpolaatiopolynomi p pisteissä x0 = 0, x1 = 1. Laske myös max, x:[0,1], |f(x)-p(x)|.

3. On haettava 1. asteen polynomi p(x, y) = cl + c2x + c3y (luvut 1, 2 ja 3 alaindekseja) joka. sopii funktioon f(x, y) = x/(1+y)-2y/(1+x) mahdollisimman hyvin pisteissä

(xi, yj) = (0.1i, 0.1j), i,j E {-1, 0, 1} siinä mielessä, että neliösumma

on mahdollisimman pieni. Kirjoita tehtävä normaalimuotoon ja ratkaise se.

4. Johda Peanon ytimen K(t) lauseke keskipistesäännön (=yhden pisteen Gauss) virhekaavassa

5. Yhtälön f(x) = x^3 - x^2 - x - 1 = 0 reaalista, positiivista ratkaisua haetaan kiintopisteiteraatiolla muodosta x = F(x), missä a) F(x) = 1 + 1/x + 1/x^2, b) F(x) = x^3 - x^2 - 1, c) F(x) = (2x^3 - x^2 + 1) / (3x^2 - 2x - 1). Tutki mitkä iteraatiot suppenevat (lähdettäessä riittävän läheltä juurta) ja määrää suppenevissa tapauksissa suppenemisen kertaluku.