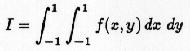
Kirjoita ensin allamainitussa järjestyksessä koepapereihin selvästi

- Num.anal.A, tentti 27.5.1994

- op.kirjan no., TEKSTATEN sukunimi ja etunimet puhuttelunimi alleviivattuna

- koulutusohjelma ja vuosikurssi (I,II,III,IV,N)

- mahdolliset entiset nimet ja koulutusohjelmat

- nimikirjoitus

1. Funktio f (x) = ln x taulukoidaan välillä [1, 2] käyttäen a) ensimmäisen asteen Lagrangen b) kolmannen asteen Hermiten interpolaatiota pisteiden xi = 1 + 1/n, i=0..n

(merkinnät: xi = x jossa i alaindeksinä)

välissä. Kuinka suureksi n on valittava, jos halutaan, että interpolointivirhe on itseisarvoltaan enintään 10^(-8)

2. Funktiosta f tiedetään, että se on kolmannen asteen polynomi ja että f (-0.1) ~ 1.12, f (0) ~ 1.46 ja f (0.1) ~ 1.28, missä funktion arvojen virhe on itseisarvoltaan enintään 0.005. Laske annetuista tiedoista f''(0) mahdollisimman tarkasti ja arvioi, kuinka suuri tämän likiarvon virhe enintään on.

3. Millaisille polynomiarvoisille funktioille f saadaan integraalille

;

tarkka arvo käytettäessä 2 x 2 pisteen Gauss-Legendren kvadratuuria? Perustele väitteesi ja määrittele myös mikä tuo kvadratuuri on.

4. Funktion f yksinkertaista nollakohtaa voi hakea kiintopisteiteraatiolla

Xk+1 = F(Xk), k = 0,1,...

(merkinnät: Xk, Xk+1 -- X, alaindekseinä k ja k+1)

missä

F(x) = x - f(x)/f'(x) - ( f''(x)/(2f'x) ) ( f(x)/f'(x) )^2

Jos iteraatio suppenee, niin mikä on suppenemisen kertaluku? Suppeneeko iteraatio aina kun lähdetään riittävän läheltä yksinkertaista nollakohtaa?

5. On haettava funktiofle f(x,y) = x^2 + xy paras mahdollinen sovitus muotoa p(x,y) = c0 + c1x + c2y siinä mielessä, että

; Kirjoita tehtävä normaalimuodossa ja ratkaise se.