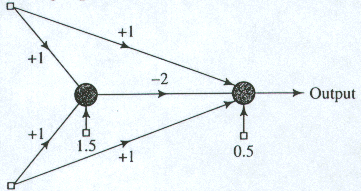
1. Tarkastellaan oheisen kuvan neuroverkkoa, jossa neuronit ovat Perceptron-yksiköitä; painot Wi on merkitty syötelinjoihin ja offset-parametrit t on kuvattu pieninä neliöinä. Aktivaatiot ovat y = U(SUM(wixi)-8) missä U on askelfunktio. Hahmottele päätösalueet (x1, x2) -tasossa ja päättele, mitä neuroverkko tekee.

2. Todista seuraava väite: mikä tahansa n:n binäärisen muuttujan xi Boolen funktio f(x1,…,xn) (missä siis sekä xi:t että f voivat saada arvokseen vain joko 0 tai 1) voidaan toteuttaa kaksikerroksisella MLP-verkolla, jossa on n syötelinjaa, yksi lähtöneuroni ja piilokerroksessa 2^n neuronia, siten että piilokerroksen painot eivät ollenkaan riipu toteutettavasta funktiosta.

3. Selosta mikä (matemaattinen) yhteys on Hopfieldin verkolla ja optimointiongelmien ratkaisulla.

4. Oletetaan 1-ulotteinen Kohosen kartta (SOM) jossa on 4 neuronia ja input-avaruus on väli [0,10]. Alkutilanteessa neuronipainot (skalaareja) ovat pisteissä m1 = 5.0, m2 = 2.0, m3 = 3.0, m4 = 8.0 (Kuva).

5. Mitä tarkoittaa back-propagationin yhteydessä ylioppiminen (overtraining), ja miten se voitaisiin välttää?