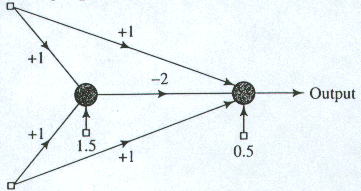

2. Tarkastellaan back-propagation-algoritmia 2-kerrosverkossa jossa on 2 neuronia sekälähtökerroksessa että piilokerroksessa ja 2 syötelinjaa. Merkitään lähtökerroksen painoja Wij ja offset-parametreja Oj, missä j=1, 2 viittaa neuroniin ja i = 1, 2 siihen piiloyksikköön mistä input tulee. Vastaavasti piilokerroksen painot ovat wkl ja offsetit Ol. Kaikkien neuronien aktivaatiofunktio on "logsig-tyyppiä eli funktio f(t)=1/(1+Exp(-t)).
Johda back-propagation-algoritmi kaikkien parametrien päivittämiseksi. Oletetaan on-line-tyyppinen opetus eli verkko oppii aina heti saadessaan uuden (input,ouput)opetusparin.
3. Anna esimerkki optimointiongelman ratkaisemisesta Hopfieldin verkolla.
4. Tarkastellaan 1-ulotteista itseorganisoivaa karttaa (SOM), jonka painovektorit ja syötteetovat 2-ulotteisia. Alkutila on kuvan 2 mukainen. Kartassa on 6 neuronia, joita opetetaanvalitsemalla syötevektorit vuorotellen kuvassa näkyvistä harmaista ruuduista. Ruutujen sisälläsyötteèt ovat tasan jakautuneet. Opetuskerroin on alpha = 0.5 ja naapurustoon kuuluvat viereiset neuronit (neuronilla 1 ja 6 vain yksi naapuri). Hahmottele painojen trajektorit ja päättele, minne ne lopulta päätyvät.

5. Mitä tarkoittaa back-propagationin yhteydessä ylioppiminen (overtraining), ja miten se voitaisiin välttää?