Tapaus 2 - Koodaus ja dekoodaus
Virike:
Tietokoneet ja muut tietotekniset laitteet esittävät käsiteltävän informaation pääsääntöisesti bittimuodossa, ts. jonoina nollia (0) ja ykkösiä (1). Bittijonona kertaalleen esitetty informaatio, data, on usein puolestaan hyödyllistä koodata, eli esittää uudestaan haluttuun sovellustarkoitukseen siten, että alkuperäinen bittijono voidaan tietyin (sovelluksesta riippuvin) edellytyksin palauttaa takaisin koodatusta bittijonosta tai sen osista, eli dekoodata alkuperäiseksi bittijonoksi.
Johdattelemme yleisen aihepiirin äärelle kahden sovelluksen kautta:
- Virheenkorjaus tiedonsiirrossa ja tiedon tallennuksessa
- Arkaluontoisen salaisuuden jako osiin
Historiallinen ja kielenkäytöllinen huomio. Ohjelmointia itseään on usein tapana kutsua "koodaukseksi", kuten vaikkapa kerrottaessa kaverille, että "naputtelin vähän koodia sisään". Ammoisina aikoina tämä tarkoitti, että kirjamellisesti napsauteltiin sähkökytkimiä halutun ohjelman lataamiseksi tietokoneen muistiin, konekielellä, bitti kerrallaan. Nykyisin vaikkapa Scala-kielellä ohjelmointi edellyttää näiltä osin huomattavasti vähemmän "koodaamista"!
Esimerkkisovellus 1: Virheenkorjaus
Aikamme saavutuksiin kuuluu vaikkapa komeiden maisemakuvien vastaanottaminen vierailta taivaankappaleilta. Ohessa esimerkkinä eräs Opportunity-mönkijän panoraamakameran 1024×1024 raakaotoksista naapuriplaneetaltamme päiväyksellä Sol 3353.

Karua seutua! Mutta miten ihmeessä kuva on saatu siirrettyä ehjänä Marsista tänne Maahan?
Useimmat tekniset haasteet karkeasti sivuuttaen, tietojenkäsittelijän näkökulmasta tehtävä palautuu siihen miten esittää kuva tai muu lähetettävä tai tallennettava informaatio vikasietoisesti siten, että haluttu informaatio voidaan purkaa esiin vaikka esitykseen olisi päässyt muutama virhe mukaan, esimerkiksi radiokanavan virhealttiuden tai tallennusvälineen fyysisen vaurioitumisen takia. Ohessa esimerkki naarmuisesta tallennusvälineestä.

Mutta mistä on kyse? Miksi kuva saapuu virheettömästi Marsista Maahan? Miksi levy soi virheettömästi vaikka siinä on naarmu? Miten insinööri suojaa lähetettävän tai tallennettavan informaation luontoäidin välinpitämättömyyttä vastaan?
Oheinen eräästä Dilbert-sarjakuvasta muodostettu yksinkertainen mustavalkokuva toimikoon esimerkkinä.

Kuva koostuu 145 rivistä ja 190 sarakkeesta siten, että jokainen alkio kuvassa on joko musta (1) tai valkoinen (0). Liittämällä rivit peräkkäin toistensa perään saadaan 145×190 = 27550 bitin jono, joka esittää kuvaa. Tältä kamerasta saatu data voisi, karkeasti yksinkertaistettuna, näyttää Marsissa.
Mutta entäpä jos lähetämme datan (bittijonon) radioteitse Maahan, tai tallennamme datan fyysiselle tallennusvälineelle, jossa bitit altistuvat virheille?
Virheet, mallinnus ja simulointi
Insinöörityön yleisiin harmeihin kuuluvat kiire sekä resurssien puute. Tässäkin tapauksessa emme valitettavasti pysty kurssin puitteissa tarjoamaan bittikanavaa Marsiin tai runsasta tallennusvälinekokoelmaa perusteellisia kokeita varten, vaan joudumme tyytymään tiedonsiirto- tai tallennuskanavan malleihin, joita voimme simuloida tietokoneella tutustuaksemme ja varautuaksemme varsinaisen todellisen ongelman haasteisiin.
Varoitus. Mallinnettaessa ja simuloitaessa luontoäidin temmellystä on insinöörin poikkeuksetta oltava varuillaan vastaako malli riittävän tarkasti todellisuutta, ja ovatko simulaatiot riittävän kattavat tukemaan tehtyjä johtopäätöksiä. Mars-lennosta tulee kallis lasku, ja insinööriltä jää ura kesken, jos tieto ei kuljekaan!
Tämän kurssin puitteissa oletamme seuraavat kaksi kanavamallia riittäviksi ohjelmoinnin harjoittelua virikkeistämään.
Malli 1: Symmetrinen riippumaton kanava
Ensimmäinen mallimme mallintaa tilannetta, jossa kanavassa on satunnaista kohinaa bittivirheitä aiheuttamassa. Oletetaan, että virheet tapahtuvat jokaisen bitin kohdalla toisista biteistä riippumattomasti, ja yksittäisen bittivirheen todennäköisyys on p. Kunkin virheen tapahtuessa bitin arvo muuttuu sen alkuperäisestä arvosta käänteiseksi. Vaihtoehtoisesti malli voidaan mieltää siten, että heitämme jokaisen bitin kohdalla kerran kolikkoa, joka tulee klaavapuoli ylöspäin todennäköisyydellä p, ja klaavan sattuessa käännämme kulloinkin tarkastellun bitin arvon. Seuraavassa esimerkkejä mitä tapahtuu eri arvoilla p mallia simuloitaessa.
|
p = 0.05

|
p = 0.1

|
|
p = 0.2

|
p = 0.4

|
|
p = 0.5

|
Malli 2: Symmetrinen purskekanava
Toinen mallimme mallintaa tilannetta jossa virheet tapahtuvat satunnaisesti purskeissa pitkin tarkasteltavaa bittijonoa. Vaihtoehtoisesti voidaan mieltää, että bittijono "naarmuuntuu" satunnaisesti siellä täällä. Määritellään virhemalli tarkemmin seuraavasti. Olkoon jonossa N bittiä. Käydään jonon bitit läpi järjestyksessä yksi kerrallaan seuraavia sääntöjä noudattaen. Jos olemme jonon alussa, tai jonossa välittömästi edeltävä bitti ei kuulu purskeeseen, kuulukoon nykyinen bitti purskeeseen todennäköisyydellä q. Jos jonossa välittömästi edeltävä bitti kuuluu purskeeseen, kuulukoon nykyinen bitti purskeeseen todennäköisyydellä 1-r. Jos bitti kuuluu purskeeseen, käännetään sen arvo käänteiseksi riippumattomasti todennäköisyydellä p. Jos bitti ei kuulu purskeeseen, säilytetään sen arvo aina ennallaan. Seuraavassa esimerkkejä mitä tapahtuu eri arvoilla p, q ja r mallia simuloitaessa.
|
p = 0.5, q = 0.01 ja r = 0.04

|
p = 0.5, q = 0.002 ja r = 0.003

|
Virheistä selviytyminen, koodaus ja dekoodaus
Yleinen keino selviytyä virheistä on esittää informaatio bittejä tuhlaillen eli redundantisti, eli esittää alkuperäinen data käyttäen hyväksi enemmän bittejä kuin varsinaisesti olisi tarpeen. Tällaista muunnosta kutsutaan datan koodaamiseksi virheistä selviytymistä varten.
Eräs yksinkertainen tapa koodata bittijono tuhlailevasti on toistokoodi, jossa jokainen alkuperäinen bitti toistetaan tietty määrä kertoja. Esimerkiksi alkuperäinen jono 10110 koodattuna 5-kertaisella toistokoodilla on 1111100000111111111100000.
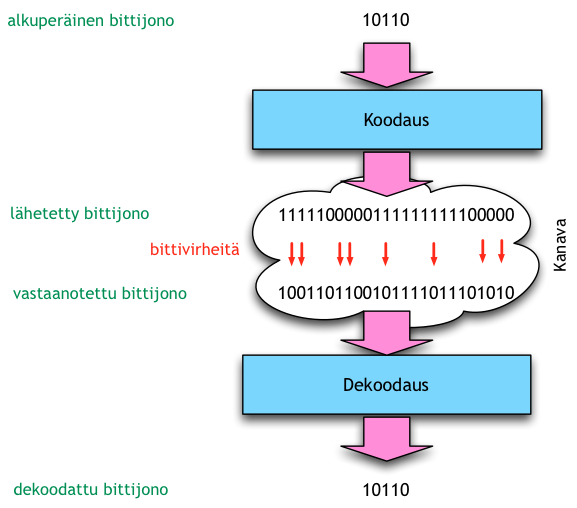
Koodaukselle käänteinen muunnos on vastaanotetun tai tallennusvälineeltä luetun bittijonon dekoodaus. Virheenkorjaussovelluksissa dekoodaus on yleisesti koodausta työläämpää, erityisesti koska koodattuihin bitteihin on saattanut siirron tai tallennuksen aikana tulla virheitä. Lisäksi jos virheitä on liikaa, dekoodaus voi epäonnistua ja tulokseksi saadaan alkuperäisestä bittijonosta poikkeava bittijono.
Esimerkiksi 5-kertaisen toistokoodin tapauksessa vastaanotettua bittijonoa tarkastellaan 5 bitin lohkoissa, ja kunkin lohkon kohdalla valitaan lohkon enemmistön bittien arvo; tällä menetelmällä alkuperäiset lähdebitit voidaan palauttaa jos ja vain jos kuhunkin lohkoon on osunut enintään 2 virhettä, muussa tapauksessa dekoodauksen tulos ei vastaa alkuperäistä bittijonoa. Esimerkiksi vastaanotetun jonon 1001101100101111011101010 jako 5 bitin lohkoihin on 10011, 01100, 10111, 10111 ja 01010. Lohko kerrallaan enemmistöarvoon dekoodaten saamme tulokseksi 10110.
Koodausteoria ja informaatioteoria
Koodausteoria ja laajemmin informaatioteoria tutkivat informaation tehokasta esittämistä eri käyttötarkoituksiin, kuten esimerkiksi yllä tarkasteltuun virheenkorjaukseen. Eräitä muita informaatioteoriassa tarkasteltuja tutkimussuuntia ovat mm. tiedon pakkaus sekä tiedon salaus ja suojaus. Jälkimmäisestä eräs esimerkki pohdittavaksi seuraavassa.
Esimerkkisovellus 2: Arkaluontoisen salaisuuden jakaminen osiin
Insinöörin toimenkuvaan kuuluu sangen usein myös organisaation tehtävien ja prosessien mahdollistavan teknisen infrastruktuurin suunnittelu. Esimerkiksi rahoitusalalla tai eräissä muissa yhteiskunnallisesti kiistanalaisissakin sovelluksissa vallitsevaksi käytännöksi on muodostunut, että organisaation mihinkään yksittäiseen toimijaan ei tule varauksetta luottaa.
Otetaan esimerkiksi vaikkapa pääsy pankkiholviin. Oletetaan, että pankkikonttorissa on k ≥ 2 kappaletta työntekijöitä, joille kullekin annetaan avain pankkiholviin. Turvallisuussyistä on kuitenkin päätetty noudattaa nk. kahden henkilön sääntöä, jolla tarkoitaan tässä tapauksessa, että mitkä tahansa kaksi edellämainituista k työntekijästä pystyvät avaamaan holvin, mutta kukaan työntekijä yksinään ei pysty avaamaan holvia. Esittäkäämme lisäksi suunnitteluvaatimuksena lukitusjärjestelmälle, että minkään yksittäisen avaimen sisältämä informaatio ei saa mitenkään auttaa avaamaan holvia. Eli jos asiattoman kulkijan käytössä on vain yksi avain, kulkija voisi aivan yhtä hyvin unohtaa avaimen olemassaolon ja pyrkiä murtamaan holvin täysin ilman avainta. Yksinkertaisuuden vuoksi oletetaan vielä, että holvi halutaan avata enintään kerran.
Pankkiholvin voidaan ajatella pelkistetyn siten, että holvin ovi avautuu jos ja vain jos ovessa olevalta numeronäppäimistöltä syötetään oikein 100-numeroinen tunnusluku. Tunnuslukua on mahdollista kokeilla vain kerran.
Halutun holvipääsyn mahdollistamiseksi 100-numeroinen tunnusluku on selvästi jaettava (koodattava) jollakin tavoin osiksi k työntekijälle siten, että mitkä tahansa kaksi osaa mahdollistavat tunnusluvun päättelyn (dekoodauksen). Eräs idea olisi vaikkapa jakaa kullekin työntekijälle karsittu tunnusluku, jossa yksi sadasta numerosta (kullekin työntekijälle eri numero!) on mustattu. Vaan täyttyvätkö sittenkään kaikki suunnitteluvaatimukset, murtopuuhia ajatellen?
Tehtäviä
- Miksi hieman naarmuinen CD-levy soi vielä virheettömästi? Entäpä jos laitamme ohuen kaistaleen maalarinteippiä levyn pintaan? Peitämme puolet levystä maalarinteipillä? Miksi kännykässä puhe välillä pätkii?
- Miksi on hyödyllistä mallintaa ja simuloida? Miksi on tärkeää, että rakennettu malli vastaa todellisuutta?
- Joskus käy nk. näppihäiriö opiskelijanumeroa, sosiaaliturvatunnusta, tai pankkisiirron viitenumeroa naputellessa, eli kone ei hyväksy syötettyä numero- ja kirjainsarjaa. Miten kone tietää, että kyseessä oli häiriö? Onko kyseessä virheen korjaus vaiko virheen havaitseminen?
- Pohdiskele miksi opiskelijanumerossa ei käytetä toistokoodausta. Kumpi vaatii enemmän tuhlausta, virheen havaitseminen vai korjaaminen?
- Tutustu EAN-viivakoodeihin ja QR-koodeihin. Käytetäänkö niissä virheenkorjausta? Toistokoodia vai muuta koodausmenettelyä?
- Paljonko tiedämme suoran kulmakertoimesta, jos tunnemme suoralta yhden pisteen? Entäpä jos tunnemme kaksi pistettä? Miten käyttäisit edellistä havaintoa hyödyksi pankkiholvin lukitusjärjestelmää laadittaessa? Miten salaisuus voitaisiin jakaa (koodata) osiin? Entäpä palauttaa (dekoodata) osista, jos mitkä tahansa ainakin kaksi osaa ovat saatavilla? Pohdiskele ratkaisua huolellisesti myös murtovarkaan näkökulmasta. Vuotaako informaatiota?
- Virheenkorjauksessa datan esityksestä tehdään suunnitelmallisesti redundantti virheistä selviytymistä varten. Monesti informaation esitysmuoto on tahattomasti redundantti. Tällöin tavoite on pakata data, jotta se vie vähemmän tilaa, ts. pakkauksen tuloksena saatu bittijono on lyhyempi kuin alkuperäinen bittijono. Eräitä yksinkertaisia menetelmiä pakata dataa ovat RLE (run-length encoding) ja Huffman-koodaus (Huffman coding). Selosta kuinka ainakin toinen näistä menetelmistä toimii. Millainen data pakkautuu selostetun menetelmän avulla hyvin? Millainen data ei pakkaudu menetelmän avulla?
- Voidaanko dataa aina pakata?
Oppimistavoitteet:
